决策论中的一些基本概念。
基本内容
- 不确定型决策的几种准则:悲观准则、乐观准则、最小后悔准则、等可能性准则与乐观系数法
- 风险型决策的最大期望收益值法(EMV)、贝叶斯决策准则及信息价值(EVPI)、决策树法
不确定型决策
决策基本要素
- 状态空间:$S=\left{S_{1}, S_{2}, S_{3} \cdots, S_{m}\right}=\left{S_{i}\right} \quad i=1, \cdots m$
- 策略空间:$A=\left{A_{1}, A_{2}, \cdots, A_{n}\right}=\left{A_{j}\right} \quad j=1, \cdots, n$
- 损益函数:$U_{i j}=u\left(S_{i}, A_{j}\right) \quad i=1,2, \cdots m ; j=1,2, \cdots n$
所以决策系统可以表示为三个主要素的函数:
$$D=D(S, U, V)$$
不确定决策例子
公司决策生产那种新商品
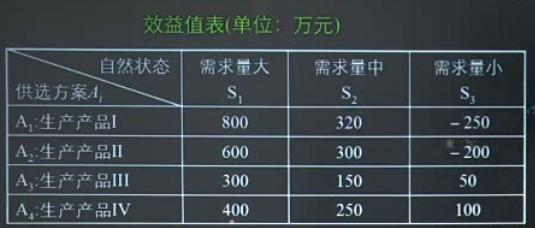
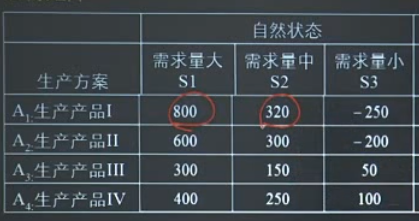
- 悲观主义准则(小中取大)
- 乐观主义准则(大中取大)
- 最小后悔值准则:编制机会损失表$r_{i j }=\left{\max {j}\left{a{i j }\right}-a_{i j}\right}$,找出每个方案的最大机会损失$Z_{i}=\max {i}\left{r{i j}\right}$,选择最小的机会损失值$Z_{l}^{*}=\min {i}\left{Z{i}\right}$
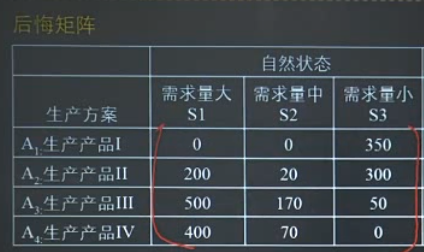
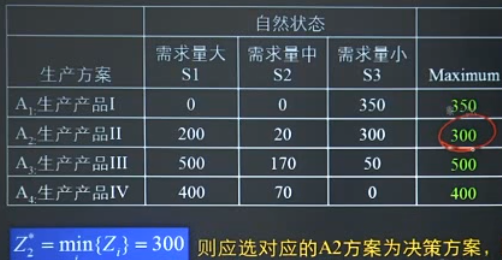
- 等可能型决策:不同状态等可能,计算平均收益
- 乐观系数法:给出乐观系数$\alpha \in[0,1]$
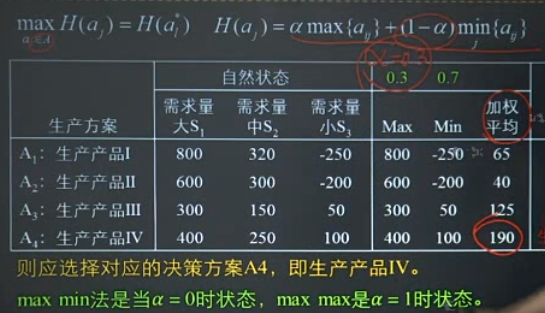
风险型决策
对发生各事件的概率已知,一般采用期望值作为决策准则。
贝叶斯决策准则及信息价值(EVPI)
已知先验概率,可以通过增加花费(信息费用)修正概率,修正概率通过贝叶斯公式得到。
