matlab模拟退火工具箱satools

​ 记录了模拟退火的原理和matlab第三方工具箱satools的使用。

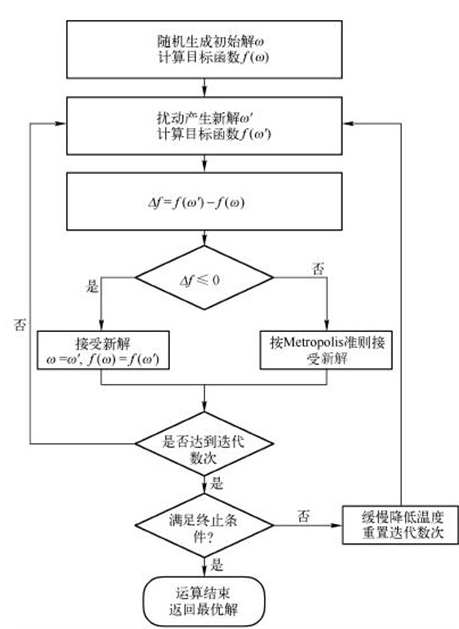
算法原理

SATOOLS使用

模拟退火主函数anneal

调用格式：

1
2
3
4
5
6
7
8
9
10
11

function [W,Ew,Wbsf,Ebsf,Tt,Et,Etarget,ert,Kt,Ebsft,Eh,M,rho,Ebin] = anneal( ...
    verbose, ...
    newstate, X, ...
    cost, moveclass, ...
    walkers, ...
    acceptrule, q, ...
    schedule, P, ...
    equilibrate, C, maxsteps, ...
    Tinit, r, ...
    Tfinal, f, maxtemps, ...
    v, bins, e)

参数说明

输入参数

• verbose：flag变量，为1时打印状态变量
• newstate：用户自定义函数,产生初始解
• X：问题的domain(解空间?)，常量
• cost：用户自定义函数，最优化的目标函数
• moveclass：用户自定义函数，用来产生新解
• walkers：正整数
• acceptrule：用户自定义函数，接受规则，工具箱也提供了几个，经常用metropolis准则
• q：acceptrule所需要的参数
• schedule：温度更新函数，可自定义
• P：schedule所需参数
• equilibrate：(平衡)可传入函数句柄或其他。当传入函数时，表示温度是否改变的判断函数
• C：equilibrate所需参数
• maxsteps：同一温度下的迭代最大次数
• Tinit：初始化函数，可自定义可使用工具箱提供函数。
• r：Tinit所需参数
• Tfinal：终止温度，可以是自定义函数，工具箱也提供，或者是数（-INF ok）
• f：参数
• maxtemps：最大温度迭代次数
• v：温度变化的快慢$[0,1]$
• bins：
• e：

输出参数

• W：每个walker的最终状态

• Ew：W对应的最终能量

• Wbsf：每个walker的best so far状态

• Ebsf：每个walker的best so far能量

• Tt(i)：每次温度步的温度记录

• Et(i)：Tt(i)对应的平均能量

• Etarget（i）：Tt(i)对应的目标平均能量，根据v计算

• ert(i)：

• kt(i)：Tt(i)对应的热平衡步数

• Ebsft(i)：Tt(i)对应的best so far能量

• Eh：能量和温度的历史记录

  • i = 1,1 + (steps*walkers)
  • Eh(i,1)：温度步的下标t
  • Eh(i,2)：t对应的温度T
  • Eh(i,3)：在温度T时的达到热平衡步数的编号j
  • Eh(i,4)：walker的编号k
  • Eh(i,5)：在T温度下,第j步，walker k对应的能量
  • Eh(i,6)：在T温度下,第j步，energy E' attempted from E

• M：

• rho：

• Ebin：

自定义函数编写

1. newstate产生初始解，

   1 2 3 4 5 6 7 8 9 10 11 12 13

   function W = PROBLEMNAME_new(X) % W = PROBLEMNAME_new(X) % See http://www.frostconcepts.com/software for information on SA Tools. % % W = PROBLEMNAME_new(X) ; % % X = behaviorally constant application data % % W = specific data about current state % % Instantiates a new state. % W = [] ; % a typical application will put state specific data here

2. cost最优化目标

   1 2 3 4 5 6 7 8 9 10

   function Ew = PROBLEMNAME_cost(X,W) % Ew = PROBLEMNAME_cost(X,W) % % X = behaviorally constant application data % % W = specific data about current state % % Ew = energy corresponding to W % Ew = rand ; % a typical application will use information from W and X to compute Ew.

3. moveclass产生新解

   1 2 3 4 5 6 7 8 9

   function W = PROBLEMNAME_perturb(X,W,Ea,T) % W = PROBLEMNAME_perturb(X,W,Ea,T) % % X = behaviorally constant application data % % W = (on input) current state, (on output) next state. % % Ea = current average energy % T = current temperature

4. 产生解空间

   1 2 3 4 5 6

   function X = PROBLEMNAME_init() % X = PROBLEMNAME_init() % % X = behaviorally constant application data % X = [] ; % a typical application will put problem domain data here